Online Layer Normalization: Derivation of Analytical Gradients
Layer Normalization is a technique developed by Ba, Kiros, and Hinton for normalizing neural network layers as a whole (as opposed to Batch Normalization and variants which normalize per-neuron). In this post I’ll show my derivation of analytical gradients for Layer Normalization using an online/incremental weighting of the estimated moments for the layer.
Background and Notation
Training deep neural networks (and likewise recurrent networks which are deep through time) with gradient descent has been a difficult problem, partially (mostly) due to the issue of vanishing and exploding gradients. One solution is to normalize layer activations, and learn the skew (b) and scale (g) as part of the learning algorithm. Online layer normalization can be summed up as learning parameter arrays g and b in the learnable transformation:
\[\begin{align} y &= g \odot z + b \\ where: z_o &= \frac{a_o - \mu_t}{\sigma_t} \\ a_o &= \sum_i{w_{oi} x_i} \\ \mu_t &= \alpha_t (\frac{1}{D} \sum_p{a_p}) + (1-\alpha_t) \mu_{t-1} \\ \sigma_t &= \alpha_t \sqrt{\frac{1}{D-1} \sum_p{(a_o - \mu_t)^2}} + (1-\alpha_t) \sigma_{t-1} \end{align}\]The vector a is the input to our LayerNorm layer and the result of a Linear transformation of x. We keep a running mean ($\mu_t$) and standard deviation ($\sigma_t$) of a using a time-varying weighting factor ($\alpha_t$).
Derivation
Due mostly to LaTeX-laziness, I present the derivation in scanned form. A PDF version can be found here.
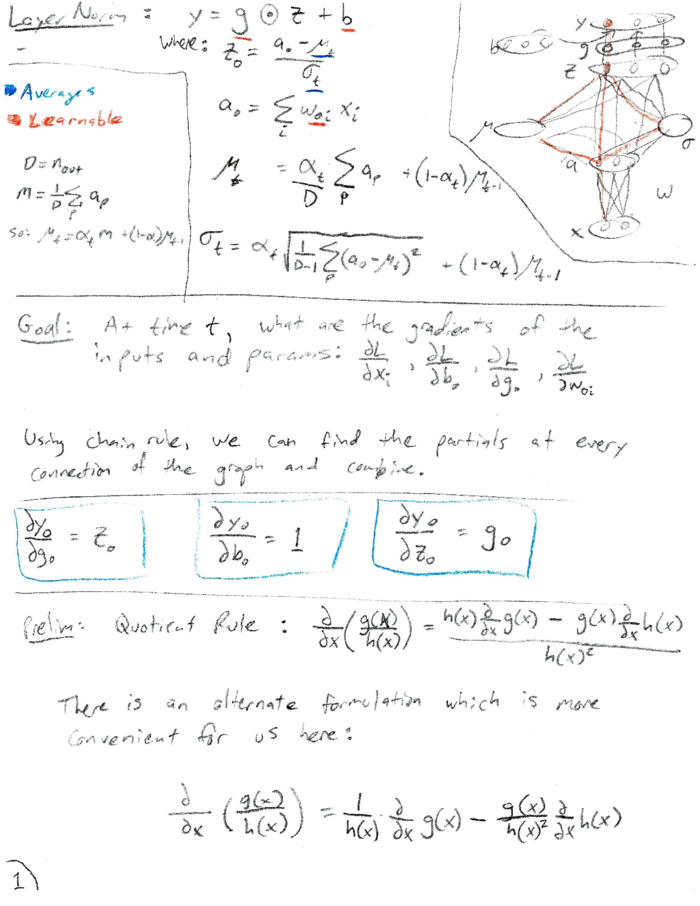



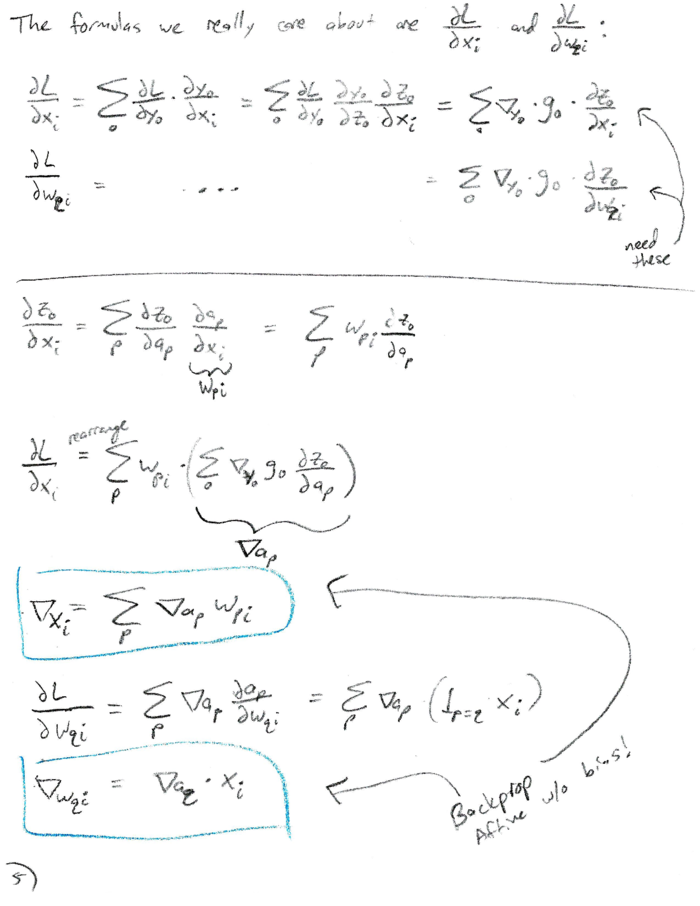

Summary
Layer normalization is a nice alternative to batch or weight normalization. With this derivation, we can include it as a standalone learnable transformation as part of a larger network. In fact, this is already accessible using the nnet convenience constructor in Transformations:
using Transformations
nin, nout = 3, 5
nhidden = [4,5,4]
t = nnet(nin, nout, nhidden, :relu, :logistic, layernorm = true)
Network:
Chain{Float64}(
Linear{3-->4}
LayerNorm{n=4, mu=0.0, sigma=1.0}
relu{4}
Linear{4-->5}
LayerNorm{n=5, mu=0.0, sigma=1.0}
relu{5}
Linear{5-->4}
LayerNorm{n=4, mu=0.0, sigma=1.0}
relu{4}
Linear{4-->5}
LayerNorm{n=5, mu=0.0, sigma=1.0}
logistic{5}
)
